Compute shaders / SmoothLife 3d

After getting 3bgl-shader to a state approximating usable, I wanted to do something to exercise it a bit, as well as try out the (relatively) new compute shaders added in OpenGL 4.3.

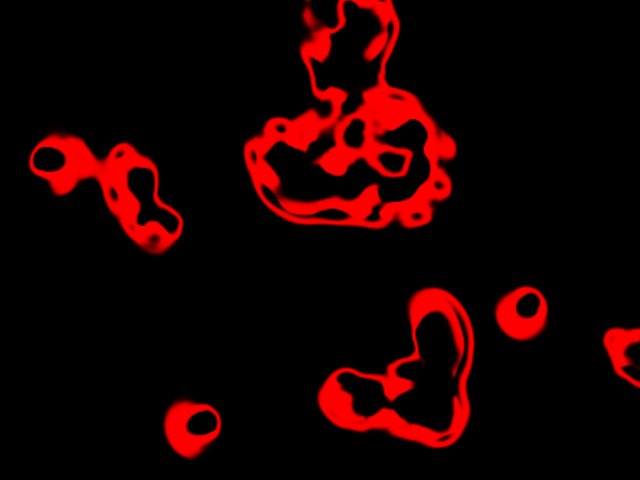
I decided to try an implementation of 3d SmoothLife, which is a generalization of the Game of Life cellular automaton to floating point, with influence from an arbitrary sized "neighborhood". The floating point values make the Hashlife optimization from normal "Life" impractical, and the wider neighborhood makes direct evaluation of the rules too expensive, particularly in 3d. Instead, the neighborhood calculations can be interpreted as convolutions with a kernel representing the shape of the neighborhood. The convolutions can then be implemented as element-wise multiplications in frequency domain, which is more efficient than direct convolution for the range of kernel sizes used even with the cost of the FFT and IFFT.

Somehow that ended up with spending a bunch of time on an educational but time consuming exploration of how FFTs work, along with experimenting on optimizing my compute-shader FFT implementations.

The general idea of 3bgl-shader seems to be working out well in practice though, in particular macros are nice for repetitive code like this. For example, I generated a macro FFT16 that takes as arguments the name of functions/macros to load/save a specific element, then I can do things like

;;; load specific rows from an image, do an FFT on them, and same to
;;; shared memory
(macrolet ((in (i)
             `(.xy (image-load tex (ivec3 x (+ y ,(* 16 i)) z))))
           (out (i re im)
             `(progn
                (setf (scratch lx ly 16 ,i) ,re)
                (setf (scratch lx ly 16 ,i t) ,im))))
  (fft16 in out))

;;; load specific elements from shared memory, do an FFT on them, and save
;;; back to the image
(macrolet ((in (i)
             `(vec2 (scratch2 lx ly 1 ,(* 16 i))))
           (out (i re im)
             `(image-store out1
                           (ivec3 (+ y ,(* 16 i)) x z)
                           (vec4 ,re ,im 0 0))))
  (fft16 in out))

without duplicating the FFT code or modifying the generator every time I wanted to change the access patterns or where it loads/saves. scratch and scratch2 are macros abstracting the layout of the elements in the shared memory.

Similarly

(defmacro with-image-vars ((x y z base-var count) &body body)
  `(let (,@(loop for i below count
                 for s =  (alexandria:format-symbol t
                                                    "~a~d" base-var i)
                 collect (list s `(image-load tex (ivec3 (+ ,y ,i)
                                                         ,x ,z)))))
     ,@body))

lets me define a set of repetitive bindings like (R0 (IMAGE-LOAD TEX (IVEC3 (+ Y 0) X Z))) to (R15 (IMAGE-LOAD TEX (IVEC3 (+ Y 15) X Z))) without getting errors where I missed/typoed a number while cut&pasting or typing them manually (which happened in one of the earlier versions, and wasted quite a bit of debugging time).

On the bad side, there is something wrong with dependency tracking in 3bgl-shader, so I have to explicitly reference some uniforms in the main shader to get them included in the output, and most error messages are very uninformative. It also could use some way to hook into slime for arglist hinting and source locations... having to search manually is pretty annoying after being used to just hitting M-..

When I finally managed to convince myself to stop trying to optimize it, I was getting about 26ms or so for a 256^3 FFT, divided into 3 passes (one for each dimension) of around 8-9ms each on my GTX780. Judging by the cuda benchmark results I've seen online I think it should be able to do about 2-3x as fast, but I'm not sure how much of that is just my implementation and how much is CUDA being more flexible than GL compute shaders.

One update of 3d smoothlife needs 2 convolutions and a pass to implement the birth/death rules using the results of the convolutions. The convolutions can share the FFT, leaving the total work at 1 FFT, 2 complex multiplies per pixel, 2 IFFTs, the running the rules per pixel. The multiplies take a few ms each, so in the final result I ended up using 1 frame per axis of the FFT and IFFTs, 1 frame for the multiplies, and 1 frame for the rules for a total of 11 frames per update. That leaves enough time for a simple draw at 60FPS as long as it isn't drawing too much (256X overdraw is a lot even for a modern GPU, particularly if it is spending most of a frame on other things). Smarter rendering is next step, since volume rendering is the other part I wanted to experiment with for this project.

Results so far: